Welcome to SACADA — Samara Carbon Allotrope Database
Nowadays the modeling of new carbon allotropes is very popular. Mistakes in classification and naming of carbon allotropes are almost inevitable due to vast amount of unorganized data. Additionally, a lot of allotropes were re-discovered many times by different research groups. Inspired by this problems we created SACADA - Samara Carbon Allotrope Database [1]. Here we gathered together all available data about 3-periodic carbon allotropes extracted from scientific literature from Web of Science and Scopus databases.
We have extracted the data of crystal structures for all unique 3-periodic carbon allotropes and indexed them in SACADA. The topological characteristics of the structures were calculated by ADS program implemented in ToposPro
[2]. The maximal symmetry embeddings of the nets were obtained by Systre program [3]. Some DFT-derived physical properties are also included in the database. All data can be sorted by clicking on the column header.
We have extracted the data of crystal structures for all unique 3-periodic carbon allotropes and indexed them in SACADA. The topological characteristics of the structures were calculated by ADS program implemented in ToposPro
[2]. The maximal symmetry embeddings of the nets were obtained by Systre program [3]. Some DFT-derived physical properties are also included in the database. All data can be sorted by clicking on the column header.SACADA content
Here we shortly describe the content of SACADA table by columns:
# (Serial Number). Serial number of the structure assigned to all chemically distinct allotropes: for example we have 4 entries for the underlying net of diamond dia that is associated also to the so called yne-diamond where for some or all bond there is a -C≡C- inserted, furthermore one of the latter (entry # 4, Y-II) is also 2-fold interpenetrated. The numbers are clickable for additional information and downloading .tar.gz archives that contains two .cif files. One of them, with _IN suffix, corresponds to the net in maximal symmetry embedding (ideal nets with C-C bonds all equal to 1.00). The other, .cif, provides the DFT-optimized structure in maximal space group symmetry.
Topology. This column contains the name for the topology of the underlying net of each carbon allotrope. The topology is clickable if the net is included in the RCSR database, and will redirect to the appropriate RCSR page.
# IN (Number of Independent Nodes). Number of topological independent nodes of the ideal nets.
Space group. Space group of the ideal nets.
Pearson. The Pearson symbol of the ideal nets give information on the Bravais lattice and the total number of atoms in the unit cell (Read more about Pearson symbol).
Density, g/cm³. Density of the structure in g/cm³ units. The first value in blue (without ref.) is calculated from our DFT optimized structure.
Gap, eV. Energy Band gap for the structure (in eV units).
Relative energy, eV/atom. Energy relative to diamond. This energy was computed according the formula:
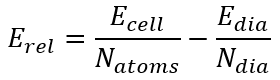
where Ecell is the allotrope unit cell energy, Natoms is the number of atoms per unit cell. Edia and Ndia are the same values for diamond.
All computations were performed using VASP package.
DFT calculations
We apply the density functional theory (DFT) approach by using the Vienna Ab Initio Simulation Package (VASP) package [6] to calculate the total energy and properties of carbon allotropes. The Generalized Gradient Approximation [7] (GGA) for exchange-correlational functional is used everywhere. The energy cutoff set to 600 eV. Fully automatic Γ-centered k-points mesh with a reciprocal-space resolution of 2π × 0.025 Å−1 is applied. We used tetrahedron method with Blöchl corrections to perform the k-point integration. The convergence thresholds are set at 10−6 eV for energy and 10−5 eV Å−1 for ionic forces. Polycrystalline elastic moduli — the bulk modulus, the shear modulus, Young’s modulus, and the Poisson’s ratio ν — have been calculated within the Voigt–Reuss–Hill [8] approximation. The Vicker’s hardness Hv has been estimated according to Oganov's model [9].
By clicking on the serial number of the structure in the table, you will be able to see the structure card, which contains the more detailed information.
Here we shortly describe the content of SACADA table by columns:
# (Serial Number). Serial number of the structure assigned to all chemically distinct allotropes: for example we have 4 entries for the underlying net of diamond dia that is associated also to the so called yne-diamond where for some or all bond there is a -C≡C- inserted, furthermore one of the latter (entry # 4, Y-II) is also 2-fold interpenetrated. The numbers are clickable for additional information and downloading .tar.gz archives that contains two .cif files. One of them, with _IN suffix, corresponds to the net in maximal symmetry embedding (ideal nets with C-C bonds all equal to 1.00). The other, .cif, provides the DFT-optimized structure in maximal space group symmetry.
Topology. This column contains the name for the topology of the underlying net of each carbon allotrope. The topology is clickable if the net is included in the RCSR database, and will redirect to the appropriate RCSR page.
# IN (Number of Independent Nodes). Number of topological independent nodes of the ideal nets.
Space group. Space group of the ideal nets.
Pearson. The Pearson symbol of the ideal nets give information on the Bravais lattice and the total number of atoms in the unit cell (Read more about Pearson symbol).
Density, g/cm³. Density of the structure in g/cm³ units. The first value in blue (without ref.) is calculated from our DFT optimized structure.
Gap, eV. Energy Band gap for the structure (in eV units).
Relative energy, eV/atom. Energy relative to diamond. This energy was computed according the formula:
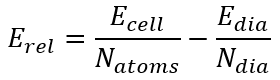
where Ecell is the allotrope unit cell energy, Natoms is the number of atoms per unit cell. Edia and Ndia are the same values for diamond.
All computations were performed using VASP package.
DFT calculations
We apply the density functional theory (DFT) approach by using the Vienna Ab Initio Simulation Package (VASP) package [6] to calculate the total energy and properties of carbon allotropes. The Generalized Gradient Approximation [7] (GGA) for exchange-correlational functional is used everywhere. The energy cutoff set to 600 eV. Fully automatic Γ-centered k-points mesh with a reciprocal-space resolution of 2π × 0.025 Å−1 is applied. We used tetrahedron method with Blöchl corrections to perform the k-point integration. The convergence thresholds are set at 10−6 eV for energy and 10−5 eV Å−1 for ionic forces. Polycrystalline elastic moduli — the bulk modulus, the shear modulus, Young’s modulus, and the Poisson’s ratio ν — have been calculated within the Voigt–Reuss–Hill [8] approximation. The Vicker’s hardness Hv has been estimated according to Oganov's model [9].
By clicking on the serial number of the structure in the table, you will be able to see the structure card, which contains the more detailed information.
© 2016 – 2023 SCTMS 
Team
References
support@sacada.info
Cite this: Angew. Chem. Int. Ed. 2016, 55, 10962–10976
Team
References
support@sacada.info
Cite this: Angew. Chem. Int. Ed. 2016, 55, 10962–10976